前言

有必要更一下我的博客文章了，我觉得独立游戏的进度没啥好放的，于是乎，我讲讲贪心算法吧

尽管说对于竞赛牲的我来说的确挺水的，但毕竟还有很多人不会么，我还是觉得讲讲比较好

尽管说，这个算法理论本身不难，就是那种做出最优解的玩意，主要难就难在实践上，换言之，就是需要多练

不多说，进入正题吧

贪心算法

定义

基础定义

贪心算法用一句话来讲，就是：

找局部最优解，然后从局部最优推导到全局最优

详细来讲就是：

贪心算法是一种在每一步选择当前状态下的最优决策，并期望通过一系列局部最优决策得到全局最优解的策略

能直接说的就这么多，可能有点抽象，那我再举个详细点的例子：

例子

比如说别人向你买东西，买完后你要找6块纸钱（默认你有无数个面额1元、面额5元的），给你个问题，是问：至少要用多少张纸币？

一般情况下，你会第一时间反应，说：这不就是常识吗？肯定至少两张了

没错，按常识来讲，确实是两张，只要选择一张面额5元的和一张面额1元的给别人就可以了

但机器不会按照所谓的常识去理解这个问题，他必须要一个严格的推理过程，也就是算法，这时候你如果不设计贪心的策略（当然，你给他爆了我就不说啥了），而是"优先使用1元"这种策略，那机器就会可能会给出错误的答案：至少六张

而使用贪心策略的话，这种就可以推出来，你告诉机器说：

当然，这只是贪心的典型例子罢了，当然，如果说面额是1元、3元、4元的，那用不了了，因为这个答案仍然是2张，就是3元+3元，贪心算法只会4元+1元+1元，得出是3张的结论，这时候就要用到DP了（这里不提了，详情看链接：DP和背包问题|真理の小屋）

至此，可以从这个例子中推出这是什么条件了吧，如果还不清楚的话，我就先写上，以便读者理解：

条件

这种能够完全成立的条件就俩个：

一、贪心选择性质
意思就是：某一步做出的局部最优选择，必然存在一个全局最优解以该选择为开头

二、最优子结构

意思就是：一个问题的最优解，它的子问题的解那必然也是最优解

如果这俩不成立的话，那或许贪心算法就可能会失败

贪心算法么其实能讲的就这么多，当然，这里看到的人可能会以为这和分治算法差不多，但其实这本质上有很大区别的，这里我就简单讲讲这俩的区别吧

和分治算法的区别

我之前没讲过这个算法，如果不知道的可以看看这个折叠，简单了解下：

那我就直接开始讲区别了：

一、贪心算法里的子问题主要是为了最优解而存在的，而分治算法的子问题是从一个大问题拆开的独立问题，就是把一个复杂的问题拆成更小的问题的

二、贪心是一步步求解的，不一定非得要搞子问题，而分治的核心是要分解、求解、合并的，必须要分解成多个子问题的，解开后也必须要合并成一个问题的解的

三、贪心的每一步都是最优的，而分治不一定

这下能看出是什么区别了吧，那我差不多该讲讲贪心的代码示例了

代码示例

示例一

洛谷的一道橙题，P4995 跳跳！，由于篇幅问题，我就不写了，详情可以看链接：P4995 跳跳！ - 洛谷

从题目中可以得知，如果要消耗体力最多，则需要从最矮的跳到最高的或者从最高的跳到最矮的，当然，是没用过的，至此，可以写出这样的代码：

n=int(input())
c,h=0,0
a=list(map(int,input().split()))
a.sort(reverse=True)
for i in range(n):
    if i%2==0:
        c+=(a[i//2]-h)**2
        h=a[i//2]
    else:
        c+=(a[-(i//2)-1]-h)**2
        h=a[-(i//2)-1]
print(c)

AC了（这是证明）：

一道你们可能没那么容易理解，于是我再来一道，以便你们理解

示例二

这是洛谷的一道黄题：P5019 [NOIP 2018 提高组] 铺设道路，同样的，链接在此：P5019 [NOIP 2018 提高组] 铺设道路 - 洛谷

这里我就拿图做示例了，简单来讲，就是填坑，就是这样子的：

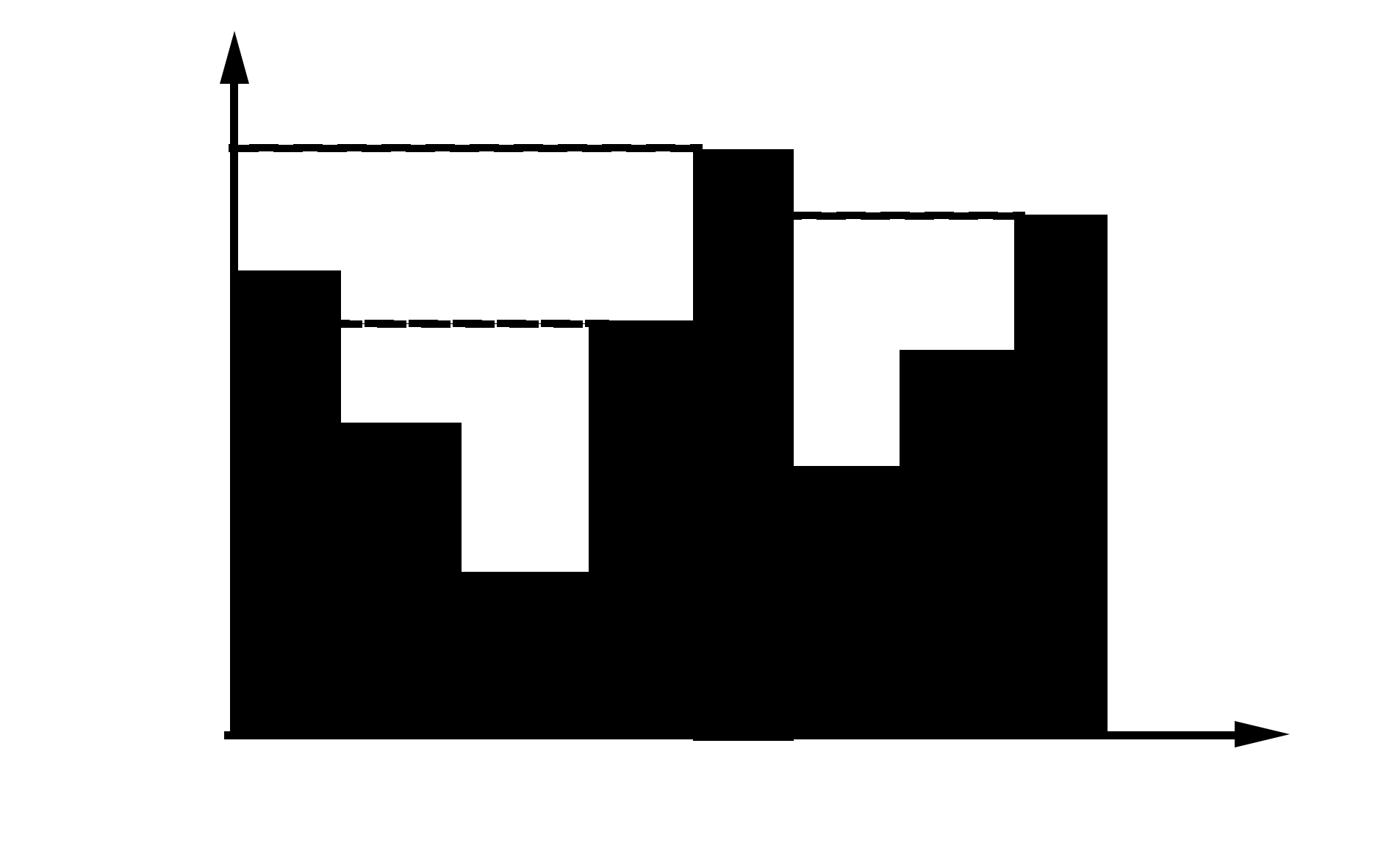
换言之，就是如果比上一个高，增加这个高度-上一个的高度，如何证明，过程在此：

假设现在这里有一个坑，但旁边又有一个坑

你肯定会选择把两个同时减1

那么小的坑肯定会被大的坑“带着”填掉

大的坑也会顺带减少a[i]-a[i-1]的深度

所以这样的策略是对的

于是就写了这样的代码：

n=int(input())
d=list(map(int,input().split()))
c=0
for i in range(1,n):
    if d[i]>d[i-1]:
        c+=d[i]-d[i-1]
c+=d[0]
print(c)

差不多了，就这样了