前言

距离上一篇文已经过去超过10天了，最近也在忙其他事，再加上我做完C#入门系列之后，就没啥好的心情去写博客，就导致更新缓慢，在这里我表示抱歉

总之，这个对我印象及其深刻，于是我将其作为第一篇算法相关的博客文章

好吧，说真的，这俩对我而言是真的头疼，为了更加深入这俩经典的树/图结构搜索算法（DFS（深度优先算法）和BFS（广度优先算法）），我选择记录下来并分享出来

事先声明，在我写作的时候我还没完全掌握所有内容，文中若有错误之处，欢迎指正

当然，在此进入正式内容之前，我觉得我有必要简单讲讲搜索算法的基本概念，之后如果还有提到的话，可以直接引用这里，也方便很多

搜索算法

定义

简单来说，搜索算法是用来解决“在解空间中寻找可行解或最优解”的一类算法

在路径规划、状态推导、数据匹配这些问题中搜索算法是非常关键的

举例

在这里，我就简单举个非常经典的例子吧，比如说迷宫，就是A到B位置呗，你要找他能到那边的方案数有多少，这里就可以用到搜索算法了

简单画个迷宫图（o为障碍，x为起点，y为终点，.为路）：

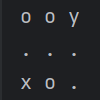
如果你肉眼去看的话，你一眼就能知道有几个方案，但是机器不一样，机器也无法像人类一样能够直观判断的，是必须依靠一套规则来系统地尝试所有可能路径的，因此这里就用到搜索算法了

这里是代码（用python的，顺带用了下DFS（深度优先算法），接下来会讲到）

def dfs(x0,y0):
    global c
    if maze[x0][y0]=='y': #如果找到终点坐标
        c+=1
        return
    for i in range(4):
        l,r=x0+direction[i],y0+direction[i+1] #往四个方向走
        if n>l>=0 and m > r >= 0 and maze[l][r]!="o" and not vis[l][r]: #如果条件达成
            vis[x0][y0]=True #设已访问
            dfs(l,r)
            vis[x0][y0]=False #回溯
    return
n,m=map(int,input().split())
maze=[]
for i in range(n):
    maze.append(list(input().split()))
vis=[[False for i in range(n)] for j in range(m)] #已访问过的点
direction=[-1,0,1,0,-1] #方向
c=0 #记方案数
for i in range(n):
    for j in range(m):
        if maze[i][j]=="x": #使用遍历找到起点坐标x
            dfs(i,j)
print("共有{}个方案".format(c)) #输出

输入：

3 3

o o y

. . .

x o .

这里是结果：

共有1个方案

讲到这里，也该差不多了解搜索算法是怎么样了，既然如此，接下来就去讲这篇文章重要的内容之一——DFS（深度优先算法）了

DFS

定义

其实前面的示例就演示过DFS了，这里就简单说一下内容：

DFS（深度优先算法）就是一种优先深入到路径最深处再回溯的搜索策略

简单来讲，就是从根开始，遍历每一个树的分支，找到每一种情况，如果没有使用剪枝来优化代码，也就是适当删无用的节点，那本质上就算是暴力搜索了

这里有些人可能没太听懂，这里顺带讲讲树（当然，由于不是重点内容，就放折叠里了）：

看到这里，大致上都能知道是什么意思，但为了防止有人说完全看不懂一类，我这里写了个框架

模板框架

这里就用伪代码模拟一下DFS：

def dfs(状态): #当前的状态
    if 当前的状态==目的的状态:
        记录结果或输出
        return
    for 寻找新状态:
        if 状态合法 and 未访问:
            vis[访问该点] #避免重复访问
            dfs(新状态)
            (vis[恢复访问])#这里看要不要回溯，要就恢复访问

这大概就是DFS的基本框架，若有特殊情况需要特殊处理，接下来我就讲个示例了

举例

之前的迷宫类型举过了，我这里举个其他的例子吧，这里我就用洛谷的题来辅助理解了：

当然，在这里，额外说一嘴，如果说你不会看cpp（也就是c++）的代码的是不太推荐的去刷洛谷的说（

以下便是洛谷原题，原题链接：P1162 填涂颜色 - 洛谷

由数字 0 组成的方阵中，有一任意形状的由数字 1 构成的闭合圈。现要求把闭合圈内的所有空间都填写成 2。例如：6×6 的方阵（n=6），涂色前和涂色后的方阵如下：

如果从某个 0 出发，只向上下左右 4 个方向移动且仅经过其他 0 的情况下，无法到达方阵的边界，就认为这个 0 在闭合圈内。闭合圈不一定是环形的，可以是任意形状，但保证闭合圈内的 0 是连通的（两两之间可以相互到达）。

0 0 0 0 0 0
0 0 0 1 1 1
0 1 1 0 0 1
1 1 0 0 0 1
1 0 0 1 0 1
1 1 1 1 1 1

0 0 0 0 0 0
0 0 0 1 1 1
0 1 1 2 2 1
1 1 2 2 2 1
1 2 2 1 2 1
1 1 1 1 1 1

输入格式

每组测试数据第一行一个整数 n(1≤n≤30)。

接下来 n 行，由 0 和 1 组成的 n×n 的方阵。

方阵内只有一个闭合圈，圈内至少有一个 0。

输出格式

已经填好数字 2 的完整方阵。

尽管说这个其实也可以用到BFS了，但DFS也可以做到，以下便是相关的讲解：

在这里，DFS的核心思路是这样的：

• 从外框开始，把所有“能从外部连通的 0”标记为3。

• 因为3代表闭环外部，因此被标记为 0 的则一定在闭环内部，于是将它们变成了2。

• 最后将所有 3 恢复为 0。

接下来就是相应的代码实现了：

代码实现

def dfs(x,y):
    global l
    if 0 <= x <= n+1 and 0 <= y <= n + 1: #如果没有查出边界
        if l[x][y]==1 or l[x][y]==3: #如果条件成立
            return
        l[x][y]=3
        for i,j in direction: #走四个方向（这里没有回溯）
            dfs(x+i,y+j)
n=int(input()) 
l=[[0 for i in range(n+2)]] #搞一个外加边缘为0的框的二维列表
direction=[(1,0),(-1,0),(0,1),(0,-1)] #方向
for i in range(n):
    l.append(list(map(int,input().split())))
    l[i+1].insert(0, 0)
    l[i+1].append(0)
l.append([0 for i in range(n+2)])
dfs(0,0) #填入外圈
for i in range(1,n+1): #将3转换为0，将0转换为2
    for j in range(1,n+1): 
        if l[i][j]==3:
            l[i][j]=0
        elif l[i][j]==0:
            l[i][j]=2
for i in range(1,n+1): #输出
    print(*l[i][1:n+1])

输入：

6

0 0 0 0 0 0

0 0 1 1 1 1

0 1 1 0 0 1

1 1 0 0 0 1

1 0 0 0 0 1

1 1 1 1 1 1

输出：

0 0 0 0 0 0

0 0 1 1 1 1

0 1 1 2 2 1

1 1 2 2 2 1

1 2 2 2 2 1

1 1 1 1 1 1

DFS这块讲的差不多了，接下来就开始讲BFS（广度优先搜索算法）

BFS

定义

BFS（广度优先搜索算法），是遍历图存储结构的一种算法

它就是以队列为核心，是从根开始，寻找一步可以到的可行点（需要合法，可能有其他条件的限制），并加入队列，然后弹出根，由依次对队列中的结点执行寻找操作，直至队列为空

这个就是非常典型的“以空间换时间”的一种算法，当然，和DFS一样，也是经典的树/图结构搜索算法

这里我简单搞个框架用来模拟下BFS是什么样的：

模板框架

这里就用伪代码模拟一下DFS（这里本质上是用递推的，但为了方便理解，还是写了方法了）：

from collections import deque

def bfs(状态): #当前的状态
    queue = deque([原始状态]) #
    visited = set([原始状态])
    
    while queue: #如果它不是空的
        当前状态 = queue.popleft() #弹出节点
        if 当前状态 == 目标状态: #如果当前状态就是目标
            记录结果或输出
            return
        for 每个可能的下一个状态:
            if 状态合法且未访问:
                visited.add(新状态)
                queue.append(新状态)

在这里肯定会有人说了，既然前文提到BFS是树/图结构搜索算法，那为何不比较同样是树/图结构的DFS呢？那在这里，我就这俩做个简单的比较了：

和DFS的区别

主要区别

1. 遍历顺序：DFS就是典型的一直走，撞到头就回退，而BFS会先搜索最近的节点，从上往下遍历

2. 数据结构：如果BFS要用到队列（就是拿队列的空间换取时间的），而DFS 通常通过递归或显式栈实现，当然在这方面个人更喜欢递归

3. 适用场景：应用场景不太一样，一个更适合找多少个方案，一个找最短路径（无权图）

用BFS一定比DFS快吗？

不一定，如果用BFS找有多少个方案的话，用队列换时间的意义是没有的，不如说用DFS更方便

当然，用DFS也不一定说比BFS快，正如前文提到DFS是遍历所有情况的（当然，即使遍历了所有情况也不一定完全正确的），所以也不能说他比BFS快

不说那么多了，以防有些没看太懂，我直接放例题了

示例

在这里，我就用最经典的洛谷题来演示下BFS

以下便是洛谷原题，原题链接：P1443 马的遍历 - 洛谷

有一个 n×m 的棋盘，在某个点 (x,y) 上有一个马，要求你计算出马到达棋盘上任意一个点最少要走几步。

输入格式

输入只有一行四个整数，分别为 n,m,x,y。

输出格式

一个 n×m 的矩阵，代表马到达某个点最少要走几步（不能到达则输出 −1）。

从某个点，最少几步上就能看出来是用BFS了，以下便是相关的讲解：

在这里，BFS的核心思路是这样的：

代码实现

from collections import deque
def bfs(sx,sy): #BFS算法部分
    global board #让BFS里的方法能够随意更改board
    direction = [ 
        (2,1),(2,-1),
        (1,2),(1,-2),
        (-2,1),(-2,-1),
        (-1,2),(-1,-2)
    ]#方向
    queue=deque() #队列，BFS最重要的部分
    board[sx][sy]=0 #起始点
    queue.append((sx, sy)) #填入队列里
    while queue: #开始BFS运算
        x,y = queue.popleft() #从队列里找节点
        step=board[x][y] #读取原本要几步
        for dx,dy in direction: #八个方向遍历
            nx,ny=x+dx,y+dy
            if 0<=nx<n and 0<=ny<m and board[nx][ny]==-1: #如果条件成立
                board[nx][ny]=step+1 #填入步数
                queue.append((nx, ny)) #将nx，ny填入队列里
    return board
n,m,x,y=map(int, input().split()) #输入
board=[[-1 for i in range(m)] for j in range(n)] #搞一个二维数组
bfs(x-1,y-1) #开始BFS
for i in board: #输出
    print(*i)

输入：

3 3 1 1

输出：

0 3 2

3 -1 1

2 1 4

至此，DFS和BFS已全部结束

总结

总而言之，DFS和BFS是搜索算法中基础也非常重要的俩个算法，他们本身也不存在说谁更好之类的，在BFS里的“用BFS一定比DFS更快吗？”中也说了一遍，而真正的关键主要在于是否匹配问题这方面：

如果需要枚举每一条路，DFS是最好的选择

如果要最短的路，而BFS就是一种非常好的方法

当然了，在你做这些玩意的时候最好先想一想是什么题，然后再对症下药，想明白了，题目自然迎刃而解（当然，除特殊情况）

这篇文章更多是我的一次梳理，难免存在理解不够深入的地方，欢迎所有人来指正或讨论